DeepSeek first gained fame because DeepSeek V2 achieved a cost of just 0.14 dollar per million tokens. At the same time, GPT-4 cost 30 dollar, and even the highly cost-effective GPT-3.5 was priced at 1.5 dollar. This breakthrough pricing sparked a price war in China, with many major tech companies slashing prices or even offering free models. However, unlike the logic of burning money for subsidies adopted by other companies, DeepSeek achieved an order-of-magnitude cost reduction through a series of technological innovations. This article introduces one of the most critical innovations behind this — MLA (Multi-Head Latent Attention).
The core mathematical trick of MLA isn’t complicated; the paper explains it in just a few sentences, leaving readers amazed at such an elegant solution. However, because it’s tightly coupled with the Transformer architecture, understanding it can be challenging. Here, I’ll simplify the explanation as much as possible so that even those unfamiliar with Transformers can grasp the brilliance of this method.
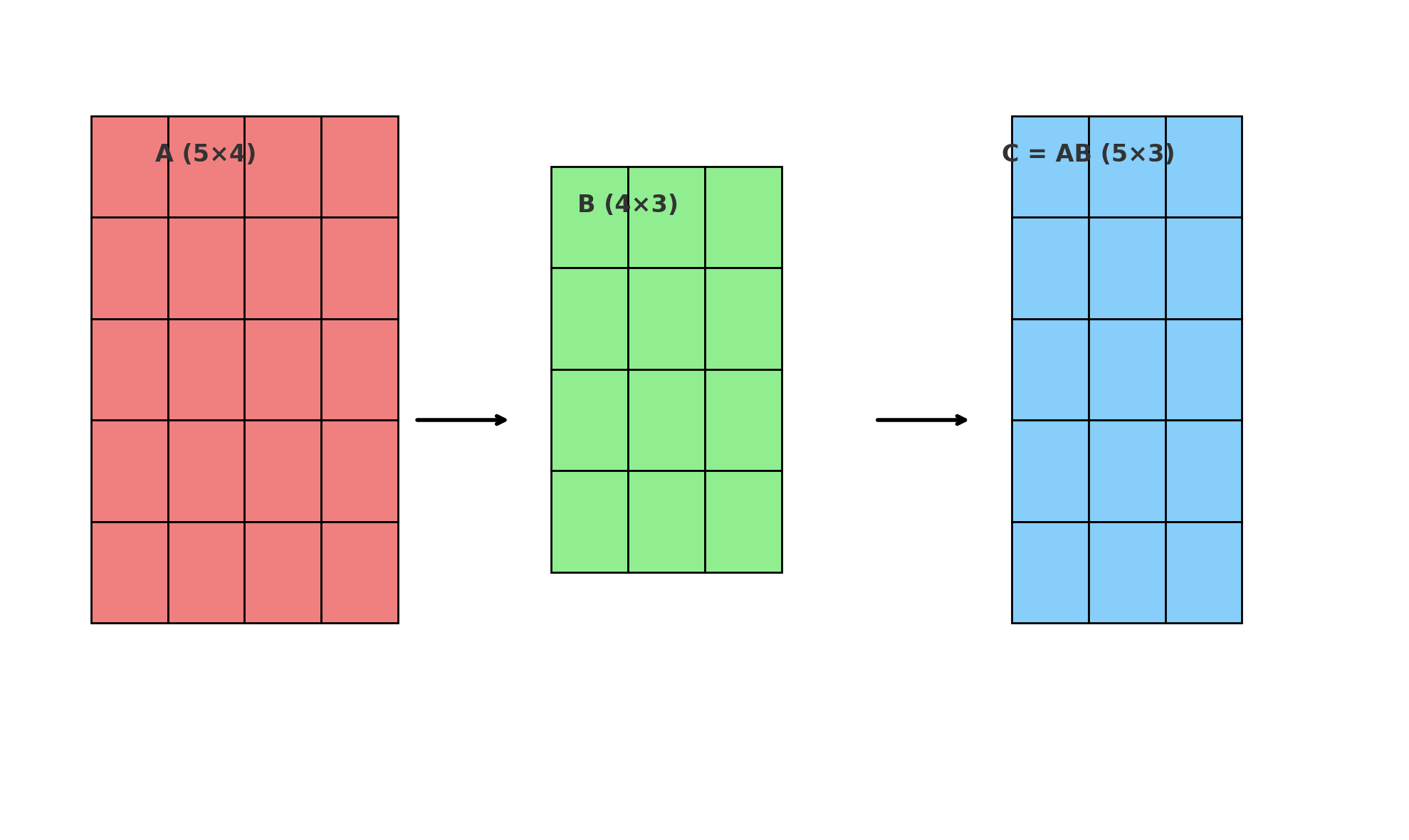
Of course, some linear algebra basics are required. If you remember that multiplying a 5×4 matrix by a 4×3 matrix results in a 5×3 matrix, you’re good to go.
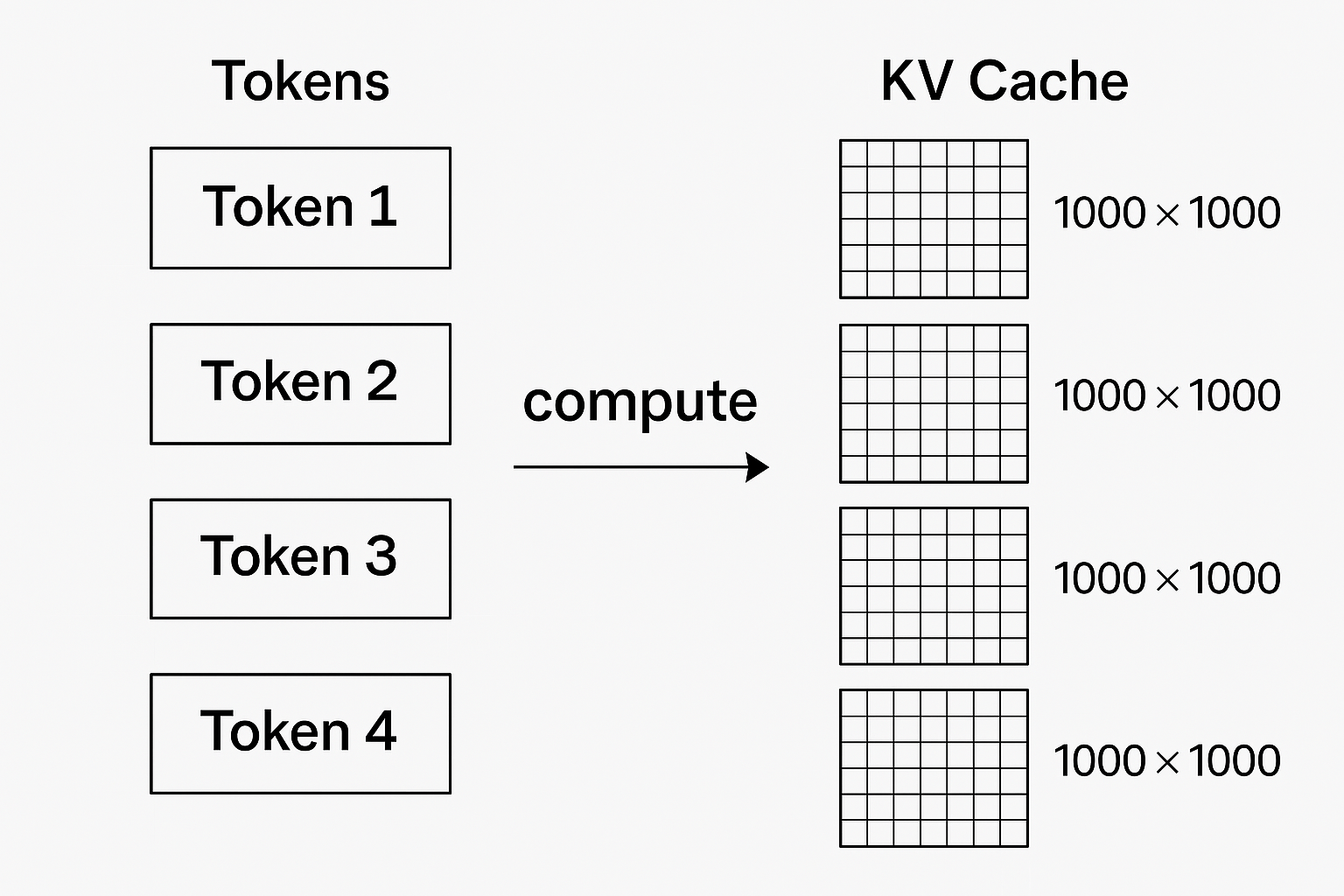
KVCache
Where is the bottleneck in large model inference costs? The answer might surprise you — it’s GPU memory. GPUs have a large number of compute units, but inference tasks are linear, generating only one token at a time. To maximize throughput and fully utilize GPU resources, as many generation tasks as possible are run simultaneously. Each task consumes a significant amount of GPU memory during inference, so to run as many tasks as possible, the runtime memory footprint must be minimized. MLA reduces the runtime memory usage of the original attention mechanism to 6.7%. That’s not a 6.7% reduction — it’s a 93.3% reduction. To put it metaphorically, this isn’t a waist cut but an ankle cut. Ignoring the model’s own memory footprint, MLA can theoretically accommodate 15 times more generation tasks under the same memory constraints.
Although the MLA paper doesn’t elaborate on the inspiration behind this, I believe they reverse-engineered it from the original KVCache, leading to a completely new attention mechanism. This brings us to the question: What is KVCache?
For each token generated, a large model needs to compute all previous tokens to determine the next one. However, tasks typically don’t end after generating one token; they continue until an end token is produced. This means the earlier tokens must be recomputed every time. KVCache addresses this by storing the intermediate results of each token’s computation, avoiding redundant calculations. Imagine each token being mapped to a 1000×1000 matrix. Is there a way to reduce the memory footprint of this matrix?
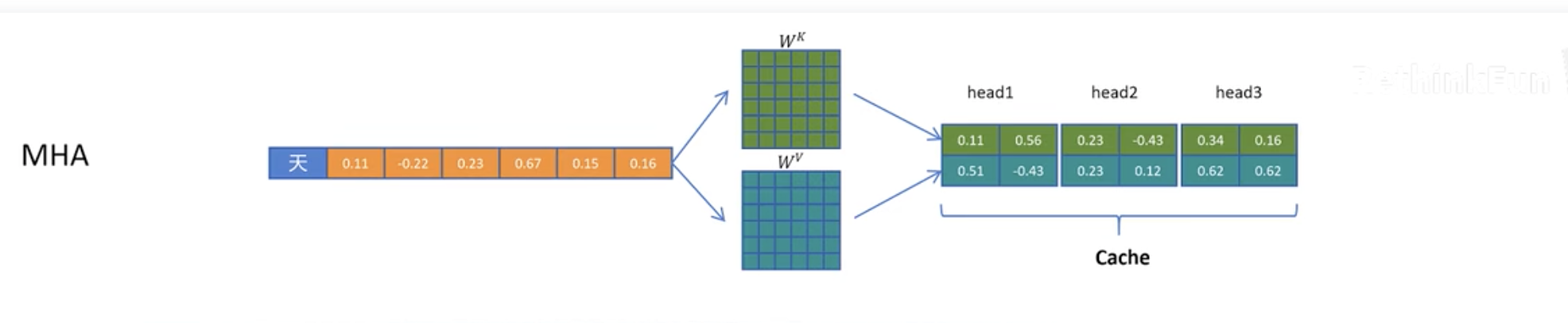
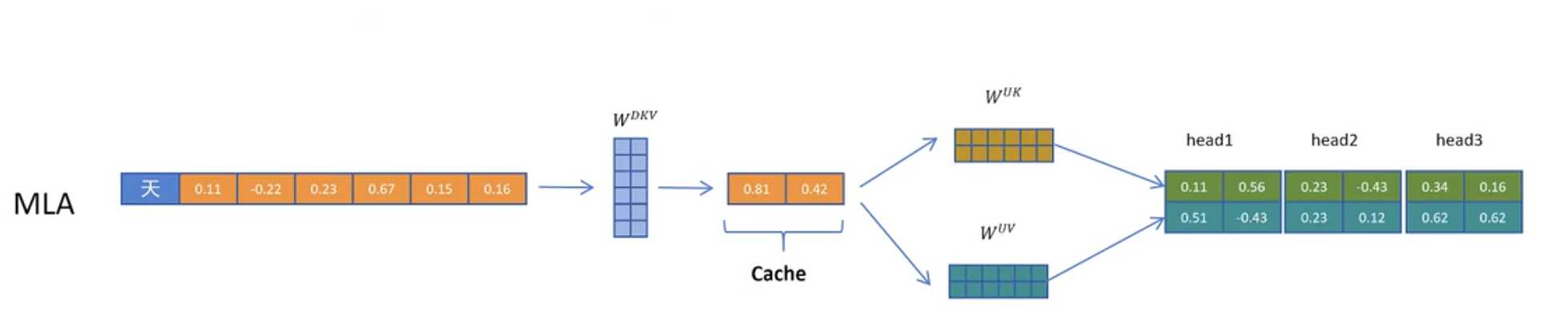
MLA
Here’s where things get interesting. We can approximate a large matrix by multiplying two smaller matrices. Remember your linear algebra: a 1000×2 matrix multiplied by a 2×1000 matrix also yields a 1000×1000 matrix, but the two smaller matrices contain only 4000 elements — just 0.4% of the original matrix’s size.
This is the core mathematical idea behind MLA. In DeepSeek V2, a token is originally mapped to a 1×16k vector. With MLA, it’s first compressed into a 1×512 vector via a compression matrix, then later decompressed into a 1×16k vector using a 512×16k decompression matrix. Here, both the compression and decompression matrices are learned during training and are fixed parts of the model, occupying constant memory. At runtime, each token’s memory footprint is reduced to just the 1×512 vector — only 3% of the original size.
A full comparison is shown below. The original MHA needs to cache the full matrix, while MLA only caches the compressed vector and reconstructs the full matrix when needed.
Is it really this perfect? Let’s revisit the original purpose of KVCache: to avoid redundant intermediate computations for tokens. While MLA compresses KVCache, it still requires a decompression step, bringing the computational cost back.
Here’s where the story gets even more fascinating. In Transformer computations, the cached intermediate result is multiplied by a decompression matrix and then an output matrix to produce the final result. Roughly speaking, the computation can be expressed as: Cache × Wdecompress × Woutput
Thanks to the associative property of matrix multiplication, we can first multiply the latter two matrices and fuse them into a single new matrix. Since Wdecompress and Woutput are fixed after training, this fusion can be precomputed with simple post-processing. The authors even describe this in the paper with the word “Fortunately”.
In other words, we initially compressed KVCache to save memory, but in actual inference, no decompression happens. Not only is memory usage drastically reduced, but the smaller matrices also decrease computational requirements.
Model Capability
However, one question remains unanswered: MLA essentially approximates a large matrix with two smaller ones, but not all large matrices can be perfectly decomposed this way. The actual search space of MLA is smaller than MHA’s, so theoretically, MLA’s model capability should be weaker. Yet, according to DeepSeek’s paper, MLA slightly outperforms MHA in evaluations.
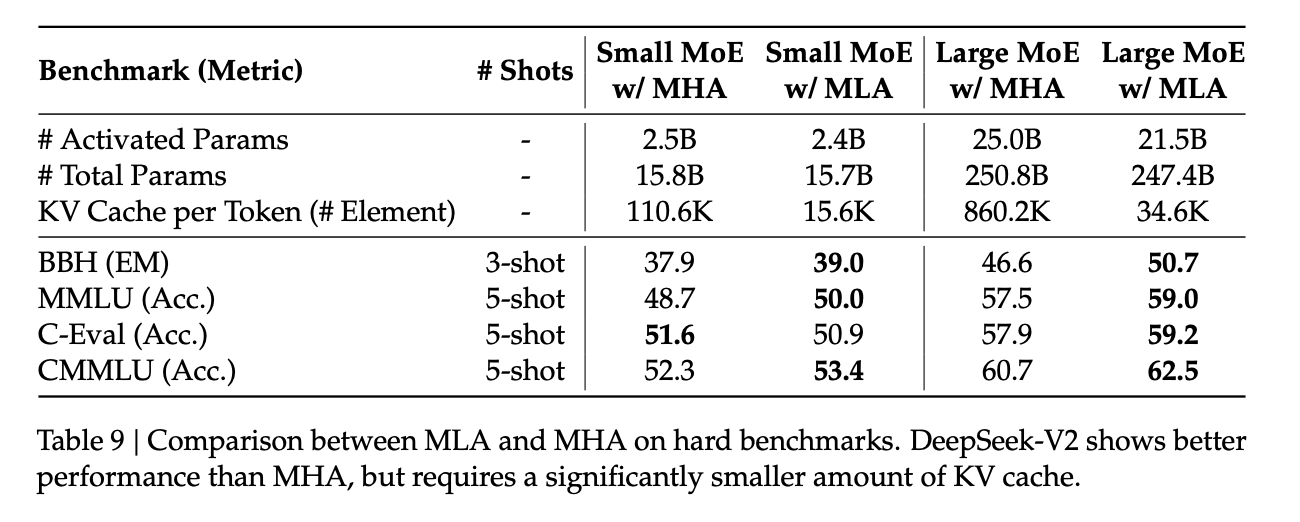
This is harder to explain. I suspect that while MLA’s search space is reduced, the probability of finding a better solution increases, allowing it to converge to a more optimal point than MHA. Additionally, although MLA’s optimization starts from MHA, the final result is a completely new attention mechanism, altering the model’s architecture. Perhaps DeepSeek has indeed discovered a more efficient attention mechanism.
Conclusion
Many performance optimizations are zero-sum games — trading GPU compute time for memory, or sacrificing model capability for cost reduction. MLA, however, achieves a drastic reduction in memory usage while also lowering computational demands and improving model performance. It’s almost unbelievable.
Another takeaway is that, having lived through China’s mobile internet era, we often assume price wars mean losing money for market share. But we forget that technological innovation should be the greatest lever of all.
This blog only covers the core idea of MLA. In practice, there are many implementation details, such as: How is rotary positional encoding handled? The fusion of K and V decompression matrices differs slightly — one applies the associative property directly, while the other requires transposition first. I highly recommend reading DeepSeek V2’s original paper. With this article as a foundation, it should be much easier to understand.
Some images in this blog are sourced from DeepSeek-v2 MLA Explanation Video. I also recommend watching this video.
